Fractions and Binomials
The binomial coefficient is defined by the next expression:
\[
\binom{n}{k} = \frac{n!}{k!(n-k)!}
\]Displaying fractions
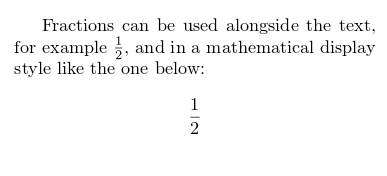

Continued fractions
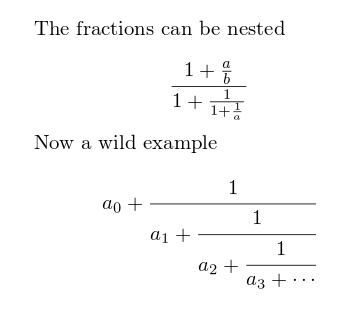
Binomial coefficients

Reference guide
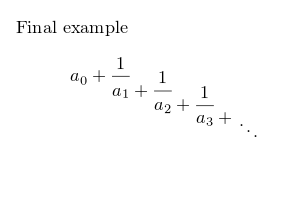
Last updated
Was this helpful?